Markdown数式完全ガイド：LaTeX基礎から応用まで徹底解説

はじめに：概要

現代の技術文書作成や学術コミュニケーションにおいて、数学的な表現を正確に記述することは極めて重要です。Markdown は軽量マークアップ言語として、LaTeX 数式構文を統合することで、文書内で数式を美しく表現する機能を提供します。学術研究者、技術ブロガー、教育関係者を問わず、Markdown での数式記述を習得すれば、文書の品質と表現力を大幅に向上させることができます。

Markdown は 2004 年に John Gruber によって作成された当初、数式表現をサポートしていませんでした。技術文書や学術執筆の需要が高まるにつれ、コミュニティは Markdown に数式を統合する方法を模索し始めました。2010 年頃に MathJax が登場し、Web 上での数式レンダリングに強力な解決策を提供。その後、より高速な KaTeX などのレンダリングエンジンも登場しました。

GitHub は 2022 年 5 月に Markdown 数式の正式サポートを発表[1]。この画期的な出来事は、Markdown 数式がニッチな需要から主流機能へと移行したことを示すものでした。現在では、主要な Markdown エディタやプラットフォームのほぼ全てが何らかの形で数式表現をサポートしており、技術文書における数学的表現の使用はかつてないほど容易になっています。

主要レンダリングエンジン紹介

現代の Markdown 数式は主に 2 つのレンダリングエンジンに依存しています：MathJax と KaTeX です。MathJax は成熟した JavaScript 表示エンジンで、LaTeX、MathML、AsciiMath 入力形式をサポートし、高い互換性と豊富な機能を備えています。KaTeX は Khan Academy が開発した高速な数式組版ライブラリで、機能は簡素化されていますが、レンダリング速度が格段に速く、リアルタイムプレビューが必要なアプリケーションに最適です。

両エンジンにはそれぞれ長所があります：MathJax はより包括的な LaTeX 構文サポートと美しいレンダリング品質を提供し、数式表現の品質が特に重要な学術文書に適しています。一方 KaTeX はその優れたパフォーマンスと即時レンダリング能力により、大量の数式を扱う対話型文書において、現代的な Web アプリケーションの第一選択肢となっています。

ToMarkdown.org の数式サポート

数ある Markdown ツールの中でも、ToMarkdown.orgは専門的な変換能力と優れた数式サポートで際立っています。このプラットフォームは標準的な LaTeX 数式構文をサポートするだけでなく、HTML 内の数学コンテンツをインテリジェントに Markdown 形式に変換する独自の機能を備えています。この機能は、既存の文書を Markdown 形式に移行する必要があるユーザー、特に複雑な数式を含む学術論文や技術文書を扱う場合に非常に貴重です。

ToMarkdown.org の数式レンダリングは現代的な Web 標準に基づいており、クロスプラットフォームでの一貫性と高品質な表示を保証します。単純なインライン数式から複雑な連立方程式まで、このプラットフォームは正確で美しいレンダリング結果を提供し、ユーザーの数学コンテンツ作成を強力にサポートします。

本ガイドの価値と特徴

本ガイドは、Markdown 数式の使用法について最も包括的で実践的なチュートリアルを提供することを目的としています。基礎的な構文から始め、応用テクニックまで段階的に解説し、主要プラットフォームの特性の違いとベストプラクティスを網羅します。豊富な実例と詳細な説明を通じて、読者は様々な環境で Markdown 数式を使用するスキルを習得できるでしょう。

他のチュートリアルと異なり、本ガイドは特に実用性と完全性を重視しています。構文規則を紹介するだけでなく、実際の業務でこれらの知識を効果的に活用する方法を示します。学術論文の複雑な方程式から技術ブログの簡潔な表現、教材の明確な提示からプロジェクト文書の専門的な表現まで、本ガイドはあらゆるシナリオで数式を自在に使いこなす手助けとなるでしょう。

基礎文法の詳細解説

Markdown 数式の基礎文法を習得することは、数学表現の世界への第一歩です。各プラットフォームによって実装に微妙な違いはあるものの、コアとなる文法規則はどの環境でも高い一貫性を保っています。本章では、インライン数式とブロックレベル数式の基本文法を詳しく解説し、今後の高度な応用に向けた土台を築きます。

インライン数式の文法

インライン数式とは、テキストの段落内に埋め込まれる数式表現で、周囲の文章と同じ行内に収まり、文章の流れを中断しません。この形式は、叙述中に簡単な数学概念や変数定義、小さな計算式を挿入するのに特に適しています。

基本文法構造

インライン数式の標準文法では、単一のドル記号を区切り文字として使用します：

これはインライン数式の例です：$E = mc^2$、これは質量とエネルギーの等価関係を示しています。

この例では、 $E = mc^2$ が数式としてレンダリングされ、周囲のテキストは通常のフォーマットのままです。ドル記号は数式内容の開始と終了をマークする役割を果たし、レンダリングエンジンにこの部分を数学文法で処理するよう指示します。

一般的なインライン数式の例

実際の使用例を通じて、インライン数式の応用場面を理解しましょう：

変数と定数の定義：数学文書では変数を定義する必要が頻繁にあります。例：「未知数を$x$、円周率を$\pi \approx 3.14159$、自然対数の底を$e \approx 2.71828$とする。」この使い方により、変数定義がより明確かつ専門的になります。

簡単な演算式：テキスト中に計算過程を示す必要がある場合、インライン数式が非常に有用です。例：「ピタゴラスの定理によれば、直角三角形の斜辺の長さは$c = \sqrt{a^2 + b^2}$で、ここで$a$と$b$はそれぞれ二つの直角辺の長さです。」

数学関数と関係：数学概念を説明する際、インライン数式は関数関係を正確に表現できます。例：「関数$f(x) = x^2 + 2x + 1$は$f(x) = (x+1)^2$と因数分解でき、これは$x = -1$に重根を持つことを示しています。」

インライン数式の組版上の注意点

インライン数式を使用する際には、いくつかの重要な組版原則に注意が必要です。まず、インライン数式は周囲のテキストの行高と調和させる必要があり、数式中の上付き文字、下付き文字、分数などによって行間が不均一になるのを避けるべきです。次に、複雑な数式はインライン形式には適しておらず、テキストの可読性に影響を与える可能性があります。

実際の使用では、インライン数式は単一の変数、簡単な演算、基本関数など比較的単純な表現に限定することをお勧めします。多重分数、大きな積分記号、行列を含む複雑な表現については、より良い表示効果を得るためにブロックレベル数式の使用を検討してください。

ブロックレベル数式の文法

ブロックレベル数式は一行または複数行を独占し、通常中央揃えで表示されます。複雑な数式表現、方程式系、特に強調したい重要な数式の表示に適しています。この形式は複雑な数学内容に十分な表示空間を提供し、数式の明瞭さと可読性を確保します。

基本文法構造

ブロックレベル数式では二重ドル記号を区切り文字として使用します：

$$
\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}
$$

この文法により、数式は独立したブロック要素としてレンダリングされ、通常中央揃えで表示され、上下のテキストとは適切な間隔が保たれます。二重ドル記号は数式内容の境界を明確に示し、レンダリングエンジンが独立した表示空間を割り当てられるようにします。

複雑な数式の例

ブロックレベル数式の真価は、複雑な数学表現を扱う際に発揮されます。以下に典型的な使用場面を示します：

積分と総和：

$$
\sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}
$$

この有名なバーゼル問題の解は無限級数の優雅な結果を示しています。ブロック形式により、この数式は視覚的に適切な重視を得るとともに、各要素が明確に表示されます。

行列と行列式：

$$
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=
\begin{pmatrix}
ax + by \\
cx + dy
\end{pmatrix}
$$

行列演算は線形代数の核心概念であり、ブロック形式は行列を明確に表示するために必要な空間を提供し、各要素が正確に整列できるようにします。

複数行の方程式系：

$$
\begin{align}
x + y &= 5 \\
2x - y &= 1
\end{align}
$$

方程式系の解法は数学における一般的な問題であり、ブロック形式を使用することで各方程式が独立した行に明確に表示され、等号が揃うため構造がより明瞭になります。

数式番号付けと参照

学術文書では、重要な数式には通常番号が付けられ、後で参照できるようになります。標準的な Markdown は直接数式番号付けをサポートしていませんが、多くの拡張機能やプラットフォームがこの機能を提供しています：

$$
E = mc^2 \tag{1}
$$

\tag{}コマンドを使用して数式に番号を付け、本文中で「式(1)に示すように」という形で参照できます。この方法は技術論文や教材で非常に一般的です。

特殊文字とエスケープ

Markdown 数式では、特定の文字が特別な意味を持つため、それらの使用方法に特に注意が必要です。ドル記号自体が数式モードの区切り文字であるため、数式中でドル記号を表示する必要がある場合は、エスケープ文字\$を使用する必要があります。

同様に、バックスラッシュ\は LaTeX でコマンドの接頭辞として使用されるため、バックスラッシュ自体を表示する必要がある場合は\\を使用します。アンダースコア_は下付き文字に、キャレット^は上付き文字に、中括弧{}はグループ化に使用され、これらの文字はすべて数式モードで特別な意味を持ちます。

これらの特殊文字の役割を理解することは、正しく数式を作成する上で極めて重要です。数式が正しくレンダリングされない場合、エスケープされていない特殊文字がないか確認することが、問題解決の第一歩となることがよくあります。

よく使われる数学記号早見表

読者がすぐに使い始められるよう、最も一般的に使用される数学記号とその LaTeX コードを以下に示します：

基本演算子：

加算：+
減算：-
乗算：\times または \cdot
除算：\div または分数 \frac{a}{b}
等号：=
不等号：\neq
大なり：>、小なり：<
以上：\geq、以下：\leq

指数と根号：

上付き文字：x^2
下付き文字：x_1
平方根：\sqrt{x}
n 乗根：\sqrt[n]{x}

分数と比率：

分数：\frac{分子}{分母}
二項係数：\binom{n}{k}

ギリシャ文字：

小文字：\alpha, \beta, \gamma, \delta, \epsilon, \pi, \sigma, \theta, \phi, \psi, \omega
大文字：\Alpha, \Beta, \Gamma, \Delta, \Pi, \Sigma, \Theta, \Phi, \Psi, \Omega

集合と論理：

属する：\in
属さない：\notin
包含：\subset
和集合：\cup
積集合：\cap
空集合：\emptyset
無限大：\infty

これらの基本記号は数学表現の基本語彙を構成し、これらを自在に使いこなすことが複雑な数式を作成する前提条件となります。使用経験を積むにつれ、これらの記号の組み合わせでほとんどすべての数学概念を表現できることに気付くでしょう。

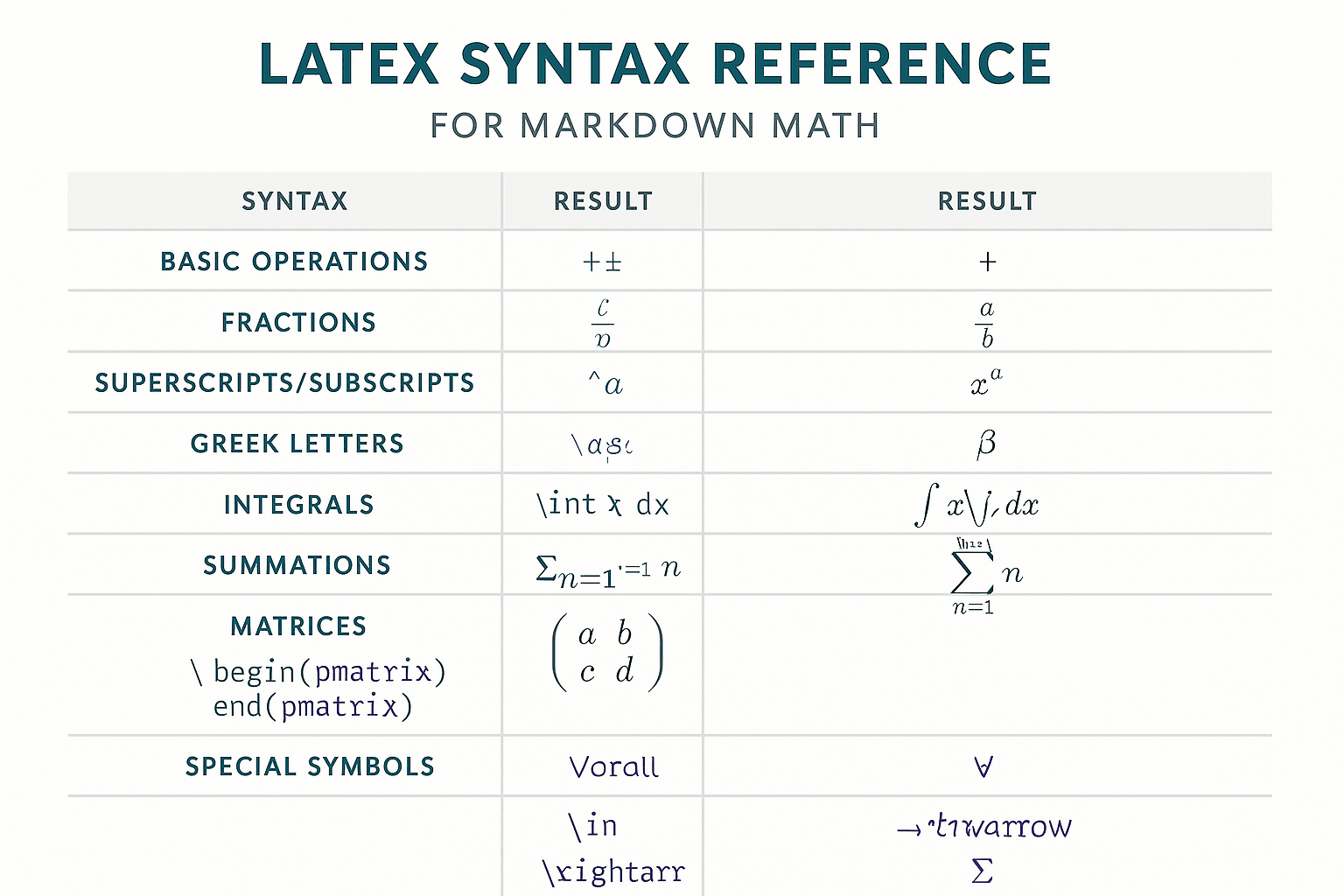
LaTeX 構文マスター

LaTeX は数式組版のゴールドスタンダードとして、Markdown 数式に強力な構文基盤を提供します。LaTeX 数式コマンドを深く理解することで、より複雑で美しい数式表現を作成できるだけでなく、LaTeX をサポートする様々なプラットフォーム間でシームレスに移行できます。本章では、LaTeX 数式構文のあらゆる側面を体系的に解説し、基礎コマンドから高度な構造まで、完全な数式表現能力を構築します。

基礎 LaTeX 数式コマンド

LaTeX 数式コマンドは厳密で優雅な構文規則に従います。各コマンドはバックスラッシュで始まり、コマンド名が続き、一部のコマンドは具体的な動作を指定するパラメータを必要とします。これらの基本コマンドの動作原理を理解することは、複雑な数式をマスターする鍵です。

テキストとフォント制御

数式モードでは、テキストの扱い方が通常のテキストモードと大きく異なります。デフォルトでは、数式モードの文字は斜体でレンダリングされ、これは数学変数の伝統的な表現方法に準拠しています。しかし、場合によっては数式中に立体テキストや特殊フォントを挿入する必要があります。

立体テキスト挿入：数式に説明文を追加する場合、\text{}コマンドを使用します：

$$
P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \text{ (ベイズの定理)}
$$

このコマンドは括弧内のテキストを立体で表示し、適切な間隔を保ちます。多言語環境では、\text{}コマンドが日本語、英語など異なる言語のテキストを正しく処理します。

数式フォント変換：LaTeX は様々な数学フォントを提供し、異なる種類の数学オブジェクトを表現します：

\mathbb{}：黒板太字、数集合に使用（例：\mathbb{R}は実数集合）
\mathcal{}：スクリプト体、集合や空間に使用
\mathfrak{}：フラクトゥール体、特定の数学分野で使用
\mathbf{}：太字、ベクトルや行列に使用
\mathrm{}：立体、関数名や定数に使用

上付き・下付き文字と装飾記号

上付き・下付き文字は数式で最も頻繁に使用される要素で、指数、添字、微分等重要な概念を表現します。LaTeX は柔軟で強力な上下付き構文を提供します。

基本上下付き構文：

上付き：^記号（例：x^2は x の 2 乗）
下付き：_記号（例：x_1は x の第 1 要素）
同時使用：x_1^2は x₁ の 2 乗

複雑な上下付き：上付き・下付き文字が複数文字を含む場合、グループ化のために中括弧が必要です：

$$
x^{2n+1} + y_{i,j}^{(k)} = \sum_{i=1}^{n} a_i x^i
$$

この例は、複数文字の上下付きの正しい書き方と、複雑な式での応用を示しています。

装飾記号とアクセント：LaTeX は豊富な装飾記号を提供します：

ハット：\hat{x}（推定値や単位ベクトル）
チルダ：\tilde{x}（近似値）
バー：\bar{x}（平均値）
ドット：\dot{x}（時間微分）
ダブルドット：\ddot{x}（2 階時間微分）
ベクトル矢印：\vec{x}（ベクトル）

高度な数学構造

数式の複雑さが増すにつれ、数学内容を整理・表示するためにより高度な構造が必要になります。LaTeX は、単純な分数から複雑な連立方程式まで、あらゆるニーズに対処する完全なツールセットを提供します。

分数と根号の高度な用法

分数は数学の最も基本的な概念の一つで、LaTeX の分数構文は単純な数値分数だけでなく、複雑な式を含む分数構造も処理できます。

入れ子分数：分子や分母自体が分数である入れ子構造：

$$
\frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{x}}}}
$$

この連分数は数論や近似理論で頻繁に現れ、LaTeX は各レベルの分数サイズを自動調整し、式全体の可読性を保証します。

根号の複雑な応用：基本的な平方根や n 乗根に加え、より複雑な根号表現：

$$
\sqrt[3]{\frac{x^2 + y^2}{x - y}} = \sqrt{\sqrt[4]{a^2 + b^2}}
$$

分数サイズ制御：分数の表示サイズを制御するコマンド：

\dfrac{}{}：ディスプレイモードの分数サイズを強制
\tfrac{}{}：テキストモードの分数サイズを強制
\cfrac{}{}：連分数用の特殊フォーマット

総和・積分・極限

数学解析における総和・積分・極限は数学的思考を表現する重要なツールです。LaTeX はこれらの概念に特化した構文を提供し、専門的で美しい表示効果を実現します。

総和記号の使用：

$$
\sum_{i=1}^{n} i^2 = \frac{n(n+1)(2n+1)}{6}
$$

\sumコマンドが総和記号を作成し、下付き文字が開始条件、上付き文字が終了条件を指定します。LaTeX は記号サイズと上下付き文字の位置を自動調整します。

積分の多様な形式：

$$
\int_0^1 x^2 dx = \frac{1}{3}, \quad \iint_D f(x,y) dA, \quad \oint_C \vec{F} \cdot d\vec{r}
$$

単一積分、二重積分、周回積分の異なる表現方法を示しています。

極限表現：

$$
\lim_{x \to 0} \frac{\sin x}{x} = 1, \quad \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e
$$

極限は\limコマンドで表現し、矢印記号\toが収束関係を示します。

行列と配列

線形代数の行列は数学の重要な構成要素で、LaTeX は様々な環境を提供し、異なるタイプの行列と配列構造を作成します。

基本行列環境：

$$
A = \begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}
$$

pmatrix環境は丸括弧付き行列を作成し、&が列区切り、\\が改行です。

異なる括弧タイプの行列：

pmatrix：丸括弧行列 ()
bmatrix：角括弧行列 []
Bmatrix：中括弧行列 {}
vmatrix：行列式 ||
Vmatrix：二重縦線行列 ||||

ブロック行列：

$$
M = \begin{pmatrix}
A & B \\
C & D
\end{pmatrix}
$$

高等線形代数で頻繁に使用されるブロック行列を LaTeX は適切に処理します。

特殊記号と関数

数学の豊かさはその膨大な記号体系に現れます。LaTeX には基本的な演算子から専門分野の特殊記号まで、ほぼ全ての常用数学記号が含まれます。

三角関数と対数関数

数学関数には専用コマンドがあり、関数名を立体表示し適切な間隔を確保します：

三角関数：

$$
\sin^2 x + \cos^2 x = 1, \quad \tan x = \frac{\sin x}{\cos x}
$$

逆三角関数：

$$
\arcsin x, \quad \arccos x, \quad \arctan x
$$

双曲線関数：

$$
\sinh x = \frac{e^x - e^{-x}}{2}, \quad \cosh x = \frac{e^x + e^{-x}}{2}
$$

対数関数：

$$
\log_a x = \frac{\ln x}{\ln a}, \quad \lg x = \log_{10} x
$$

集合論記号

集合論は現代数学の基礎で、LaTeX は完全な集合論記号サポートを提供します：

基本集合演算：

$$
A \cup B, \quad A \cap B, \quad A \setminus B, \quad A^c
$$

関係記号：

$$
x \in A, \quad A \subset B, \quad A \subseteq B, \quad A \supset B
$$

特殊集合：

$$
\mathbb{N}, \quad \mathbb{Z}, \quad \mathbb{Q}, \quad \mathbb{R}, \quad \mathbb{C}
$$

論理記号

数理論理の記号は計算機科学や数学基礎で広く使用されます：

論理接続詞：

$$
P \land Q, \quad P \lor Q, \quad \neg P, \quad P \implies Q, \quad P \iff Q
$$

量化子：

$$
\forall x \in \mathbb{R}, \quad \exists y \in \mathbb{N}
$$

数式整列と複数行表現

複雑な数学的導出を扱う際、複数の数式を整列表示したり、長い数式を複数行に分割する必要が頻繁に生じます。LaTeX はこれらのニーズを満たす強力な整列環境を提供します。

align 環境の使用

align環境は複数行数式整列の最も一般的なツールです：

$$
\begin{align}
(x+y)^2 &= x^2 + 2xy + y^2 \\
&= x^2 + y^2 + 2xy \\
&= (x^2 + y^2) + 2xy
\end{align}
$$

この例では、&記号が整列点をマークし、通常等号の前に置かれ、全ての等号が垂直に整列します。

連立方程式の表現

連立方程式は数学の一般的な構造で、LaTeX は複数の表現方法を提供します：

cases 環境の使用：

$$
f(x) = \begin{cases}
x^2 & \text{if } x \geq 0 \\
-x^2 & \text{if } x < 0
\end{cases}
$$

線形連立方程式：

$$
\begin{align}
2x + 3y &= 7 \\
x - y &= 1
\end{align}
$$

これらの高度な構造をマスターすれば、単純な代数演算から複雑な数学解析、基礎的な幾何関係から深遠な抽象代数まで、ほぼ全てのタイプの数学表現を扱えるようになります。LaTeX の強みはその一貫性と拡張性にあり、基本原理を理解すれば、様々な複雑な数学組版要求に容易に対応できます。

プラットフォーム対応比較

Markdown プラットフォームごとに数式サポートのレベルには顕著な違いがあり、これらの差異は構文の互換性だけでなく、レンダリング品質、パフォーマンス、ユーザーエクスペリエンスなど多岐にわたります。各プラットフォームの特徴と制限を理解することは、適切な作業環境を選択する上で極めて重要です。本章では主要プラットフォームの数式サポート状況を詳細に分析し、異なる環境下での適切な選択を支援します。

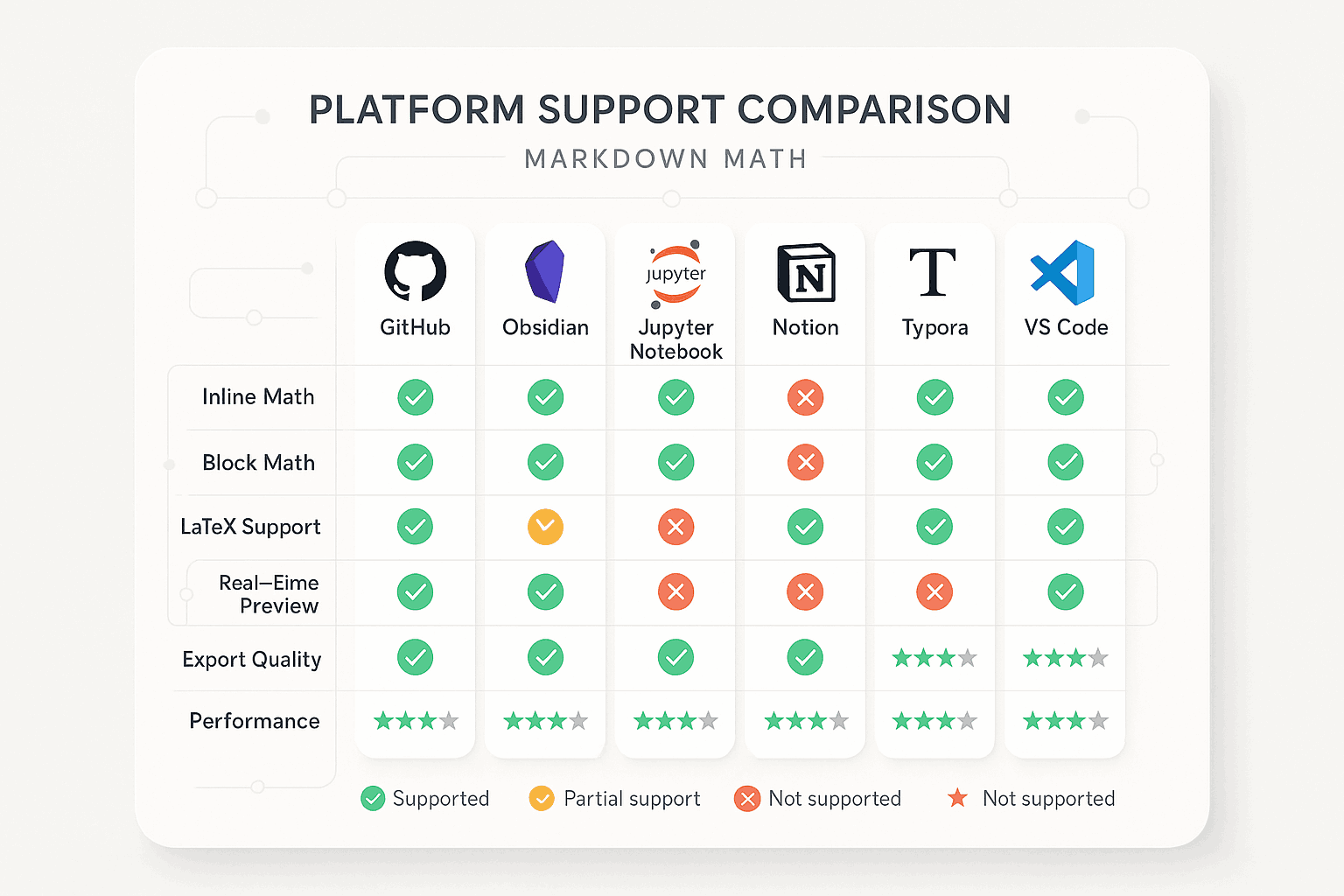
GitHub の数式サポート

GitHub は 2022 年 5 月に正式に数式サポートを導入[2]、この重要なアップデートはコードホスティングプラットフォームが学術的・技術的文書への親和性を高めた画期的な一歩となりました。GitHub の数式実装は MathJax レンダリングエンジンを基盤としており、比較的完全な LaTeX 構文サポートを提供しています。

GitHub の構文特徴

GitHub は標準的なドル記号デリミタ構文を採用し、インラインとブロックの 2 モードをサポート：

インライン数式：単一ドル記号で囲む（例： $E = mc^2$ ） ブロック数式：二重ドル記号で囲み、独立行で表示

GitHub の実装は LaTeX 標準に厳密に準拠しており、他の LaTeX 対応環境で作成した数式を変更せずに GitHub で使用可能です。この互換性は、特に数学的アルゴリズムや科学計算に関わるオープンソースプロジェクトのドキュメント管理において極めて重要です。

サポート機能範囲

GitHub の数式サポートは主要な LaTeX 数学コマンドの大部分をカバー：

基本数学構造：分数、根号、上下付き文字、総和、積分等のコア機能を完全サポート。複雑なネスト構造も正しくレンダリングされ、ほとんどの技術文書の要件を満たします。

行列と配列：pmatrix、bmatrix、vmatrixなど各種行列環境をサポートし、線形代数関連の式を扱えます。

特殊記号：ギリシャ文字、数学演算子、集合論記号、論理記号なども良好にサポート。

複数行数式：align環境やcases環境が正常動作し、複雑な数式配置と方程式系の表現が可能。

使用制限と注意事項

GitHub の数式サポートはかなり充実していますが、以下の制限に注意が必要：

レンダリング性能：MathJax はクライアント側でレンダリングを行うため、多数の数式を含むページでは読み込み遅延が発生する可能性があります。特に数式が密集した技術文書で顕著です。

モバイル体験：モバイルデバイスでは複雑な数式が正しく表示されない場合があり、特に画面が小さい場合、長い数式が画面からはみ出すことがあります。

キャッシュ機構：GitHub はレンダリング結果をキャッシュしますが、場合によっては数式の更新が即座に反映されず、強制リフレッシュが必要なケースがあります。

Obsidian の数式機能

知識管理ツールとして専門的な Obsidian は、数式に対して優れたサポートを提供しています。MathJax を基盤とした数式機能は標準 LaTeX 構文をサポートするだけでなく、いくつかの独自拡張機能も備えています。

リアルタイムプレビュー体験

Obsidian の最大の強みはリアルタイムプレビュー機能です。編集モードで数式が即時レンダリングされ、ユーザーは入力しながら最終的な数式効果を確認できます。この即時フィードバックは数学コンテンツの作成効率を大幅に向上させ、特に頻繁に数式を編集する学術作業者に適しています。

編集モードのインテリジェントヒント：数式編集時に構文ハイライトとエラー表示を提供し、構文エラーの迅速な識別と修正を支援します。数式構文が正しくない場合、エディタは明確なエラー表示を行い、可能な場合は修正提案も示します。

プレビューモードの最適化レンダリング：プレビューモードでは最適化されたレンダリングアルゴリズムを使用し、数式の表示品質とパフォーマンスを最高の状態に保ちます。複雑な数式もクリアな表示効果を維持します。

高度な機能サポート

Obsidian は他のプラットフォームでは利用できない高度な LaTeX 機能をサポート：

カスタムマクロ定義：ユーザーは独自の LaTeX マクロを定義でき、頻繁に使用する数式の入力を簡素化できます。例えば\newcommand{\R}{\mathbb{R}}で実数集合記号を簡単に入力可能。

化学式サポート：mhchem 拡張により、Obsidian は化学方程式や分子構造をレンダリングでき、化学・生物学関連のノートに有用です。

図表統合：数式と図表ツールを統合でき、同一ドキュメント内で数学式と可視化図表を混在させられます。

プラグインエコシステム

Obsidian の豊富なプラグインエコシステムは数式機能をさらに拡張：

LaTeX Suite プラグイン：ショートカット、自動補完、テンプレート機能など、より便利な LaTeX 入力体験を提供。

Math Booster プラグイン：数式の編集と表示機能を強化し、追加の数学記号と書式オプションを提供。

Export プラグイン：数式を含むノートを PDF、HTML 等の形式にエクスポートし、数式の完全性を保持します。

Jupyter Notebook の数式レンダリング

データサイエンスと科学計算の標準ツールである Jupyter Notebook は、数式に対して本質的な需要と優れたサポートを備えています。その数式機能はドキュメント説明に役立つだけでなく、コードと数学理論を結合する重要な架け橋です。

コードとのシームレス統合

Jupyter Notebook の独自性は数式と実行可能コードを完璧に統合できる点：

理論と実践の結合：Markdown セルで数学理論を記述し、コードセルで対応するアルゴリズムを実装。この結合方式により数学概念の学習と応用がより直観的になります。

動的数式生成：Python コードで LaTeX 数式文字列を動的に生成し、Markdown セルでレンダリング可能。パラメータ化された数学式に特に有用です。

計算結果の数学的表現：SymPy などの記号計算ライブラリは LaTeX 形式の数学式を直接出力でき、Notebook の表示システムにシームレスに統合されます。

科学計算の専門的サポート

科学計算分野での広範な応用により、Jupyter Notebook は数式に対して特別な最適化を実現：

NumPy と SciPy 統合：数値計算結果を直接数学式表示に変換でき、結果の表示と分析が容易です。

Matplotlib 統合：同一 Notebook 内で数学式と科学グラフを混在させ、完全な科学レポートを作成可能。

マルチメディアサポート：静的な数式だけでなく、widgets を使用したインタラクティブな数学的可視化もサポートします。

エクスポートと共有機能

Jupyter Notebook は複数のエクスポートオプションを提供し、異なる形式でも数式が正しく表示されることを保証：

PDF エクスポート：LaTeX エンジンを通じて出版品質の高品質 PDF ドキュメントを生成。

HTML エクスポート：MathJax を含む HTML ファイルを生成し、任意の最新ブラウザで正しく数式を表示。

スライドモード：Notebook をプレゼンテーションに変換可能で、数式はプレゼン過程でクリアな表示効果を維持します。

Notion の数式使用

現代的なコラボレーションツールである Notion は、数学コンテンツ専用設計ではありませんが、その数式機能は大多数のユーザーの基本ニーズを満たせます。Notion の数式は KaTeX を基盤としており、高速なレンダリング性能と良好なユーザー体験を提供します。

ユーザーフレンドリーな入力方式

Notion は数式入力体験に多くの最適化を施し、使用ハードルを低減：

ビジュアルエディタ：Notion は数式のビジュアル編集インターフェースを提供し、ユーザーはボタンクリックで一般的な数学記号を挿入可能で、複雑な LaTeX コマンドを記憶する必要がありません。

リアルタイムプレビュー：数式編集時、Notion はリアルタイムでレンダリング結果を表示し、ユーザーは即座に数式の最終効果を確認できます。

テンプレートとショートカット：Notion は一般的な数式テンプレートを提供し、分数、根号、積分などの一般的な構造を迅速に挿入可能です。

コラボレーション機能の数学サポート

コラボレーションプラットフォームとして、Notion の数式機能は特にチーム使用シナリオを考慮：

コメントと議論：チームメンバーは数式を含むコンテンツにコメントや議論を追加でき、数学コンテンツの共同編集をサポートします。

バージョン履歴：Notion は数式の編集履歴を保存し、数式の変更過程を追跡可能で、学術協力に特に重要です。

権限制御：異なるユーザーに対して数学コンテンツのアクセスと編集権限を設定でき、重要な数式の安全性を確保します。

機能制限と代替方案

Notion の数式機能は実用的ですが、専門的な数学ツールと比較すると以下の制限があります：

構文サポート範囲：KaTeX ベースの実装のため、一部の高度な LaTeX 機能、特に専門的な数学パッケージやカスタムコマンドがサポートされない場合があります。

複雑数式の処理：非常に複雑な数学式の場合、Notion の性能が影響を受け、レンダリング速度が低下する可能性があります。

エクスポート形式制限：ドキュメントエクスポート時、数式の書式が変化する場合があり、特に特定形式へのエクスポートでは数式情報が失われる可能性があります。

その他主要プラットフォーム比較

上記主要プラットフォーム以外にも、様々なツールが異なるレベルの数式サポートを提供：

Typora

WYSIWYG 型 Markdown エディタである Typora は優れた数式サポートを提供：

即時レンダリング：数式入力時、Typora は即座に LaTeX コードをレンダリング済み数式に変換し、真の WYSIWYG 体験を提供。

エクスポート品質：Typora の PDF エクスポート機能は高品質な数式を生成でき、正式文書作成に適しています。

テーマサポート：異なるテーマは数式に対して異なるスタイル設定を持ち、ユーザーは最適な表示効果を選択可能です。

VS Code

適切な拡張により、VS Code も強力な数式サポートを提供：

Markdown Preview Enhanced：この拡張は VS Code に完全な数式レンダリング機能を追加し、リアルタイムプレビューをサポート。

LaTeX Workshop：専用 LaTeX 拡張で、完全な LaTeX 編集とコンパイル環境を提供。

カスタム設定：ユーザーは必要に応じて数式のレンダリングエンジンと表示スタイルを設定可能です。

オンラインエディタ

多くのオンライン Markdown エディタも数式サポートを提供：

StackEdit：ブラウザベースの Markdown エディタで、リアルタイム数式プレビューをサポート。

Dillinger：シンプルなオンラインエディタで、基本的な数式機能を提供。

HackMD：コラボレーション型 Markdown エディタで、数式を含むドキュメントの共同編集をサポート。

プラットフォーム選択アドバイス

適切なプラットフォームの選択には複数の要素を考慮：

使用シナリオ：学術執筆には Obsidian や Jupyter Notebook が、チームコラボレーションには Notion や GitHub がより適している場合があります。

技術要件：LaTeX 構文サポートの完全性を重視するユーザーは MathJax ベースのプラットフォームを選択すべきです。

性能ニーズ：高速レンダリングが必要なシナリオでは KaTeX ベースのプラットフォームを考慮。

統合ニーズ：コードや他のツールとの統合が必要な場合は Jupyter Notebook や VS Code を検討。

各プラットフォームの特徴と制限を理解することで、異なる作業環境下で最適な選択を行い、数学コンテンツの品質と効率を最高の状態に保つことができます。

レンダリングエンジン詳細解説

数式の最終的な表示品質は、基盤となるレンダリングエンジンに大きく依存します。現在主流のレンダリングエンジンには MathJax と KaTeX の 2 種類があり、それぞれ特徴と適したシナリオがあります。これらのレンダリングエンジンの動作原理と特性を深く理解することで、様々な環境下で最適な選択を行い、数式表示を最適化することが可能になります。

MathJax vs KaTeX 比較

MathJax と KaTeX は、数式レンダリング技術の異なる発展方向を代表しています。MathJax は機能の完全性と互換性を追求する一方、KaTeX はパフォーマンスと速度の最適化に特化しています。

MathJax の特徴と利点

MathJax は Web 数式レンダリングエンジンの先駆けとして、長年の発展を経て非常に成熟しています：

機能の完全性：MathJax はほぼ全ての LaTeX 数学コマンドをサポートしており、多くの高度な機能や拡張パッケージも含みます。この包括的なサポートにより、複雑な学術文書を LaTeX 環境から Web 環境へシームレスに移行できます。

多形式サポート：LaTeX 以外に、MathML や AsciiMath 入力形式もサポートしており、様々な背景のユーザーに柔軟な選択肢を提供します。

高品質なレンダリング：MathJax のレンダリング品質は専門的な数学組版ソフトウェアに匹敵し、特に複雑な数学構造を扱う際に優れた視覚効果を維持できます。

カスタマイズ性：MathJax は豊富な設定オプションを提供し、ユーザーは必要に応じてレンダリング動作、フォント選択、出力形式など多方面を調整できます。

KaTeX の特徴と利点

KaTeX は Khan Academy によって開発され、Web 環境のパフォーマンス要件に特化して最適化されています：

レンダリング速度：KaTeX の最大の利点は極めて高速なレンダリング速度です。MathJax と比較して、KaTeX のレンダリング速度は一桁速く、大量の数式を含むページで特に重要です。

サーバーサイドレンダリング：KaTeX はサーバーサイドでの事前レンダリングをサポートし、ページ読み込み前に数式処理を完了できるため、ユーザー体験をさらに向上させます。

軽量設計：KaTeX のファイルサイズは MathJax より遥かに小さく、ネットワーク転送負荷を軽減し、特にモバイルデバイスやネットワーク環境が劣悪な状況に適しています。

モダンなアーキテクチャ：KaTeX はより現代的な JavaScript アーキテクチャを採用しており、現代のフロントエンドフレームワークとの統合がスムーズです。

パフォーマンスと互換性分析

レンダリングエンジンを選択する際、パフォーマンスと互換性は最も重要な考慮要素です。異なるアプリケーションシナリオでは、これら 2 つの側面に異なる要件があります。

パフォーマンス比較テスト

実際の使用において、レンダリングエンジンの性能差は主に以下の点に現れます：

初期ロード時間：KaTeX のライブラリファイルサイズは約 100KB であるのに対し、MathJax の完全版は 1MB を超える場合があります。ネットワーク条件が限られている状況では、この差がページの初回読み込み速度に顕著な影響を与えます。

数式レンダリング速度：100 の数式を含むページの場合、KaTeX は通常数十ミリ秒でレンダリングを完了しますが、MathJax では数百ミリ秒以上かかる場合があります。

メモリ使用量：KaTeX のメモリ占有量は通常 MathJax より 30-50%低く、リソースが制限されたデバイスで特に重要です。

互換性の考慮

互換性は主に LaTeX 構文のサポート範囲とブラウザ互換性に関係します：

LaTeX 構文サポート：MathJax がサポートする LaTeX コマンド数は KaTeX を大幅に上回ります。高度な LaTeX 機能を使用するユーザーにとって、MathJax が唯一の選択肢となる場合があります。

ブラウザ互換性：両エンジンとも現代のブラウザをサポートしていますが、MathJax は古いバージョンのブラウザに対するサポートが優れています。

モバイルデバイスサポート：KaTeX はモバイルデバイス上で通常より良好なパフォーマンスを発揮し、特にローエンドデバイスで顕著です。

選択アドバイス

異なる使用シナリオに基づき、以下の選択建議を提供します：

MathJax を選択する場合：

完全な LaTeX 構文サポートが必要
文書に複雑な数学構造が含まれる
レンダリング品質への要求が極めて高い
複数の入力形式をサポートする必要がある

KaTeX を選択する場合：

レンダリング速度への要求が高い
ページに大量の数式が含まれる
主にモバイルデバイスで使用する
サーバーサイドレンダリングが必要

実践応用ケーススタディ

理論知識は実際の応用を通じて初めて真に習得できます。本章では、典型的なアプリケーションシナリオを通じて、Markdown 数式を実務で効果的に使用する方法を紹介します。これらのケースは学術執筆から技術文書まで様々なニーズをカバーし、読者に直接参考にできる実践経験を提供します。

学術論文執筆

学術論文は数式に対する要求が最も厳しく、正確な数学表現だけでなく学術規範に準拠した書式も必要です。

定理と証明の表現

数学論文では、定理、補題、証明などの構造を明確に識別する必要があります：

**定理 1**：任意の実数 $a, b, c$ について、$a^2 + b^2 = c^2$ ならば、辺の長さが $a, b, c$ である直角三角形が存在する。

**証明**：三角形の三辺の長さをそれぞれ $a, b, c$ とし、$c$ を最長辺とする。余弦定理によれば：

$$
c^2 = a^2 + b^2 - 2ab\cos C
$$

$a^2 + b^2 = c^2$ ならば：
$$
2ab\cos C = 0
$$

$a, b > 0$ であるから、$\cos C = 0$ すなわち $C = 90°$ となる。したがって三角形は直角三角形である。 $\square$

複雑な方程式系の処理

学術論文では複雑な方程式系を提示する必要が頻繁にあります：

$$
\begin{align}
\frac{\partial u}{\partial t} &= \alpha \frac{\partial^2 u}{\partial x^2} + f(x,t) \\
u(0,t) &= g_1(t) \\
u(L,t) &= g_2(t) \\
u(x,0) &= h(x)
\end{align}
$$

この形式は偏微分方程式とその境界条件、初期条件を明確に表示しています。

技術文書作成

技術文書の数式は通常、アルゴリズム原理の説明、性能分析、またはパラメータ計算に使用されます。

アルゴリズム複雑度分析

**時間計算量分析**：

クイックソートの平均時間計算量は $O(n \log n)$ であり、$n$ はソート対象要素の数である。

最悪の場合、入力配列が既にソートされているとき、クイックソートの計算量は $O(n^2)$ に退化する：

$$
T(n) = T(n-1) + O(n) = O(n^2)
$$

一方、平均的な場合、分割統治法により：

$$
T(n) = 2T(n/2) + O(n) = O(n \log n)
$$

機械学習の数式

機械学習文書では、数式がモデル原理の説明に使用されます：

**線形回帰モデル**：

仮説関数：$h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n$

コスト関数：
$$
J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2
$$

勾配降下法更新規則：
$$
\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta)
$$

教材作成

教材では数学的概念を段階的に紹介する必要があり、数式の提示は明確で理解しやすいものでなければなりません。

概念説明と例題

**導関数の定義**：

関数 $f(x)$ の点 $x_0$ における導関数は以下のように定義される：

$$
f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}
$$

**例題**：$f(x) = x^2$ の $x = 2$ における導関数を求めよ。

**解答**：
$$
\begin{align}
f'(2) &= \lim_{h \to 0} \frac{(2+h)^2 - 2^2}{h} \\
&= \lim_{h \to 0} \frac{4 + 4h + h^2 - 4}{h} \\
&= \lim_{h \to 0} \frac{4h + h^2}{h} \\
&= \lim_{h \to 0} (4 + h) \\
&= 4
\end{align}
$$

高度なテクニックとベストプラクティス

基礎文法の習得はあくまでスタート地点であり、真のプロフェッショナルとしての実力は高度なテクニックの活用とベストプラクティスの遵守に現れます。本章では、数式の品質と効率を向上させるための高度な技術を紹介します。

複雑な数式の構成

非常に複雑な数学的表現に直面した場合、合理的な構成と分解が鍵となります：

中間変数の活用

$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$、$B = \begin{pmatrix} e & f \\ g & h \end{pmatrix}$ とすると

行列積は：
$$
AB = \begin{pmatrix}
ae + bg & af + bh \\
ce + dg & cf + dh
\end{pmatrix}
$$

導出過程の段階的表示

$$
\begin{align}
\int_0^1 x^2 e^x dx &= \left[ x^2 e^x \right]_0^1 - \int_0^1 2x e^x dx \\
&= e - 2\int_0^1 x e^x dx \\
&= e - 2\left( \left[ x e^x \right]_0^1 - \int_0^1 e^x dx \right) \\
&= e - 2(e - (e - 1)) \\
&= e - 2
\end{align}
$$

パフォーマンス最適化の技術

大量の数式を含む文書では、パフォーマンス最適化が重要になります：

過度なネストの回避

// 推奨しない：過度なネスト
$$
\frac{\frac{\frac{a}{b}}{\frac{c}{d}}}{\frac{\frac{e}{f}}{\frac{g}{h}}}
$$

// 推奨：中間変数の使用
$x = \frac{a}{b} \cdot \frac{d}{c}$、$y = \frac{e}{f} \cdot \frac{h}{g}$ とすると

元の式 = $\frac{x}{y}$

適切な数式番号付け

重要な数式は参照用に番号を付ける：

$$
E = mc^2 \tag{1}
$$

式 (1) に基づき、次の計算が可能...

クロスプラットフォーム互換性

異なるプラットフォームで数式が正しく表示されることを確認：

プラットフォーム固有の拡張回避

// プラットフォーム固有の拡張コマンドは避ける
// 互換性を確保するため標準LaTeX構文を使用

テストと検証

公開前に、ターゲットプラットフォームで数式の表示をテストし、レンダリング問題がないことを確認。

ツールとリソースの推奨

仕事を成し遂げるには、まず道具を整えることが重要です。適切なツールの選択は、数式作成の効率と品質を大幅に向上させます。

オンラインエディタ推奨

ToMarkdown.org：プロフェッショナルな Markdown ツールプラットフォームとして、ToMarkdown.orgは優れた数式編集体験を提供するだけでなく、強力なフォーマット変換機能を備えています。特に HTML から Markdown への変換機能は、数式を含む複雑な文書をインテリジェントに処理し、コンテンツ移行に多大な利便性をもたらします。

Upmath：数式専用のオンラインエディタで、リアルタイムプレビューと LaTeX コード生成機能を提供。

CodeCogs：数式のオンライン編集と画像生成サービスを提供し、LaTeX をサポートしていない環境への数式埋め込みに適しています。