
Introduction and Overview
In modern technical writing and academic communication, the accurate expression of mathematical formulas is crucial. As a lightweight markup language, Markdown integrates LaTeX math syntax, providing users with the ability to elegantly display mathematical expressions in documents. Whether you are an academic researcher, technical blogger, or educator, mastering math formula syntax in Markdown will significantly enhance the quality and effectiveness of your documentation.
The Evolution of Markdown Math Formulas
When Markdown was first created by John Gruber in 2004, it did not include support for math formulas. As the demand for technical documentation and academic writing grew, the community began exploring methods to integrate mathematical expressions into Markdown. Around 2010, the emergence of MathJax provided a powerful solution for rendering math formulas on the web, followed by faster rendering engines like KaTeX.
In May 2022, GitHub officially announced support for Markdown math formulas [1], a milestone event that marked the transition of Markdown math formulas from a niche requirement to a mainstream feature. Today, almost all major Markdown editors and platforms offer some form of math formula support, making the use of mathematical expressions in technical documentation more convenient than ever.
Introduction to Mainstream Rendering Engines
Modern Markdown math formulas primarily rely on two rendering engines: MathJax and KaTeX. MathJax is a mature JavaScript display engine that supports LaTeX, MathML, and AsciiMath input formats, offering high compatibility and rich functionality. KaTeX, developed by Khan Academy, is a fast math typesetting library. Although its features are relatively simplified, it renders significantly faster, making it particularly suitable for applications requiring real-time previews.
These two engines each have their advantages: MathJax provides more comprehensive LaTeX syntax support and more refined rendering effects, making it ideal for academic documents with high requirements for mathematical expression quality; KaTeX, with its exceptional performance and instant rendering capabilities, has become the preferred choice for modern web applications, especially in interactive documents that need to handle large numbers of math formulas.
Math Formula Support on ToMarkdown.org
Among the many Markdown tools, ToMarkdown.org stands out for its professional conversion capabilities and excellent math formula support. The platform not only provides standard LaTeX math syntax support but also has the unique ability to intelligently convert mathematical content in HTML to Markdown format. This feature is invaluable for users who need to migrate existing documents to Markdown format, especially when dealing with academic papers or technical documents containing complex mathematical expressions.
ToMarkdown.org's math formula rendering is based on modern web standards, ensuring cross-platform consistency and high-quality display results. Whether it's simple inline formulas or complex multi-line equation systems, the platform delivers accurate and aesthetically pleasing rendering results, providing reliable technical support for users' mathematical content creation.
The Value and Features of This Guide
This guide aims to provide readers with the most comprehensive and practical tutorial on using Markdown math formulas. Starting from the most basic syntax, we will gradually delve into advanced application techniques, covering the characteristic differences and best practices of all major platforms. Through numerous practical examples and detailed explanations, readers will be able to master the skills of using Markdown math formulas in various environments.
Unlike other tutorials, this guide places special emphasis on practicality and completeness. We not only introduce syntax rules but, more importantly, demonstrate how to effectively apply this knowledge in real-world work. From complex equations in academic papers to simple expressions in technical blogs, from clear presentations in teaching materials to professional displays in project documentation, this guide will help you use math formulas with ease in various scenarios.
Detailed Basic Syntax
Mastering the basic syntax of Markdown math formulas is the first step into the world of mathematical expressions. Although different platforms may have slight variations in specific implementations, the core syntax rules remain highly consistent across environments. This chapter will detail the basic syntax of inline and block-level math formulas, laying a solid foundation for subsequent advanced applications.
Inline Math Formula Syntax
Inline math formulas are mathematical expressions embedded within text paragraphs. They remain on the same line as the surrounding text without interrupting its continuity. This format is particularly suitable for inserting simple mathematical concepts, variable definitions, or small calculation formulas into narratives.
Basic Syntax Structure
The standard syntax for inline math formulas uses a single dollar sign as a delimiter:
This is an inline formula: $E = mc^2$, demonstrating the mass-energy equivalence.
In this example, $E = mc^2$ will be rendered as a math formula, while the surrounding text remains in regular format. The dollar signs mark the beginning and end of the mathematical content, telling the rendering engine that this part needs to be processed according to math syntax.
Common Inline Formula Examples
Let's understand the application scenarios of inline formulas through a series of practical examples:
Variable and Constant Definitions: In mathematical documents, we often need to define variables. For example: "Let $x$ be the unknown, $\pi \approx 3.14159$ be the pi, and $e \approx 2.71828$ be the base of natural logarithms." This usage makes variable definitions clearer and more professional.
Simple Arithmetic Expressions: Inline formulas are very useful when displaying calculation processes in text. For example: "According to the Pythagorean theorem, the hypotenuse length of a right triangle is $c = \sqrt{a^2 + b^2}$, where $a$ and $b$ are the lengths of the two legs."
Mathematical Functions and Relations: When describing mathematical concepts, inline formulas can accurately express functional relationships. For example: "The function $f(x) = x^2 + 2x + 1$ can be factored as $f(x) = (x+1)^2$, indicating that the function has a double root at $x = -1$."
Typesetting Considerations for Inline Formulas
Several important typesetting principles should be noted when using inline formulas. First, inline formulas should maintain harmony with the line height of the surrounding text, avoiding uneven line spacing caused by superscripts, subscripts, or fractions in the formula. Second, complex formulas are not suitable for inline form as they may affect text readability.
In practice, it is recommended to limit inline formulas to relatively simple expressions, such as single variables, simple operations, or basic functions. For complex expressions containing multi-level fractions, large integral symbols, or matrices, block-level formulas should be considered for better display effects.
Block-Level Math Formula Syntax
Block-level math formulas occupy one or more lines, usually centered, and are suitable for displaying complex mathematical expressions, equation systems, or important formulas that need special emphasis. This format provides ample display space for complex mathematical content, ensuring clarity and readability.
Basic Syntax Structure
Block-level math formulas use double dollar signs as delimiters:
$$
\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}
$$
This syntax renders the formula as an independent block-level element, usually centered, with appropriate spacing from the surrounding text. The double dollar signs clearly mark the boundaries of the mathematical content, allowing the rendering engine to allocate independent display space for it.
Complex Formula Examples
The true value of block-level formulas lies in handling complex mathematical expressions. Here are some typical application scenarios:
Integrals and Summations:
$$
\sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}
$$
This famous solution to the Basel problem demonstrates the elegant result of an infinite series. The block-level format gives this formula the visual emphasis it deserves while ensuring clear display of each element.
Matrices and Determinants:
$$
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=
\begin{pmatrix}
ax + by \\
cx + dy
\end{pmatrix}
$$
Matrix operations are central to linear algebra. The block-level format provides the necessary space for clear matrix display, ensuring each element is accurately aligned.
Multi-Line Equation Systems:
$$
\begin{align}
x + y &= 5 \\
2x - y &= 1
\end{align}
$$
Solving equation systems is a common problem in mathematics. The block-level format allows each equation to be clearly displayed on a separate line, with aligned equal signs making the structure more apparent.
Formula Numbering and Referencing
In academic documents, important formulas often need numbering for subsequent references. Although standard Markdown does not directly support formula numbering, many extensions and platforms provide this functionality:
$$
E = mc^2 \tag{1}
$$
The \tag{} command can add numbering to formulas, which can then be referenced in the text as "as shown in formula (1)." This practice is extremely common in technical papers and teaching materials.
Special Characters and Escaping
In Markdown math formulas, certain characters have special meanings and require special attention in their usage. The dollar sign itself is a delimiter for math mode. If a dollar sign needs to be displayed in a math formula, the escape character \$ should be used.
Similarly, the backslash \ is used in LaTeX for command prefixes. To display a backslash itself, \\ should be used. The underscore _ is used for subscripts, the caret ^ for superscripts, and curly braces {} for grouping—all these characters have special meanings in math mode.
Understanding the roles of these special characters is crucial for correctly writing math formulas. When a formula fails to render correctly, checking for unescaped special characters is often the first step in troubleshooting.
Quick Reference for Common Math Symbols
To help readers get started quickly, here are some of the most commonly used math symbols and their LaTeX codes:
Basic Operators:
- Addition:
+ - Subtraction:
- - Multiplication:
\timesor\cdot - Division:
\divor using fractions\frac{a}{b} - Equal to:
= - Not equal to:
\neq - Greater than:
>, less than:< - Greater than or equal to:
\geq, less than or equal to:\leq
Exponents and Roots:
- Superscript:
x^2 - Subscript:
x_1 - Square root:
\sqrt{x} - nth root:
\sqrt[n]{x}
Fractions and Ratios:
- Fraction:
\frac{numerator}{denominator} - Binomial coefficient:
\binom{n}{k}
Greek Letters:
- Lowercase:
\alpha, \beta, \gamma, \delta, \epsilon, \pi, \sigma, \theta, \phi, \psi, \omega - Uppercase:
\Alpha, \Beta, \Gamma, \Delta, \Pi, \Sigma, \Theta, \Phi, \Psi, \Omega
Sets and Logic:
- Belongs to:
\in - Does not belong to:
\notin - Subset:
\subset - Union:
\cup - Intersection:
\cap - Empty set:
\emptyset - Infinity:
\infty
These basic symbols form the fundamental vocabulary of mathematical expressions. Mastering their usage is a prerequisite for writing complex math formulas. As your experience grows, you'll find that combinations of these symbols can express almost all mathematical concepts.
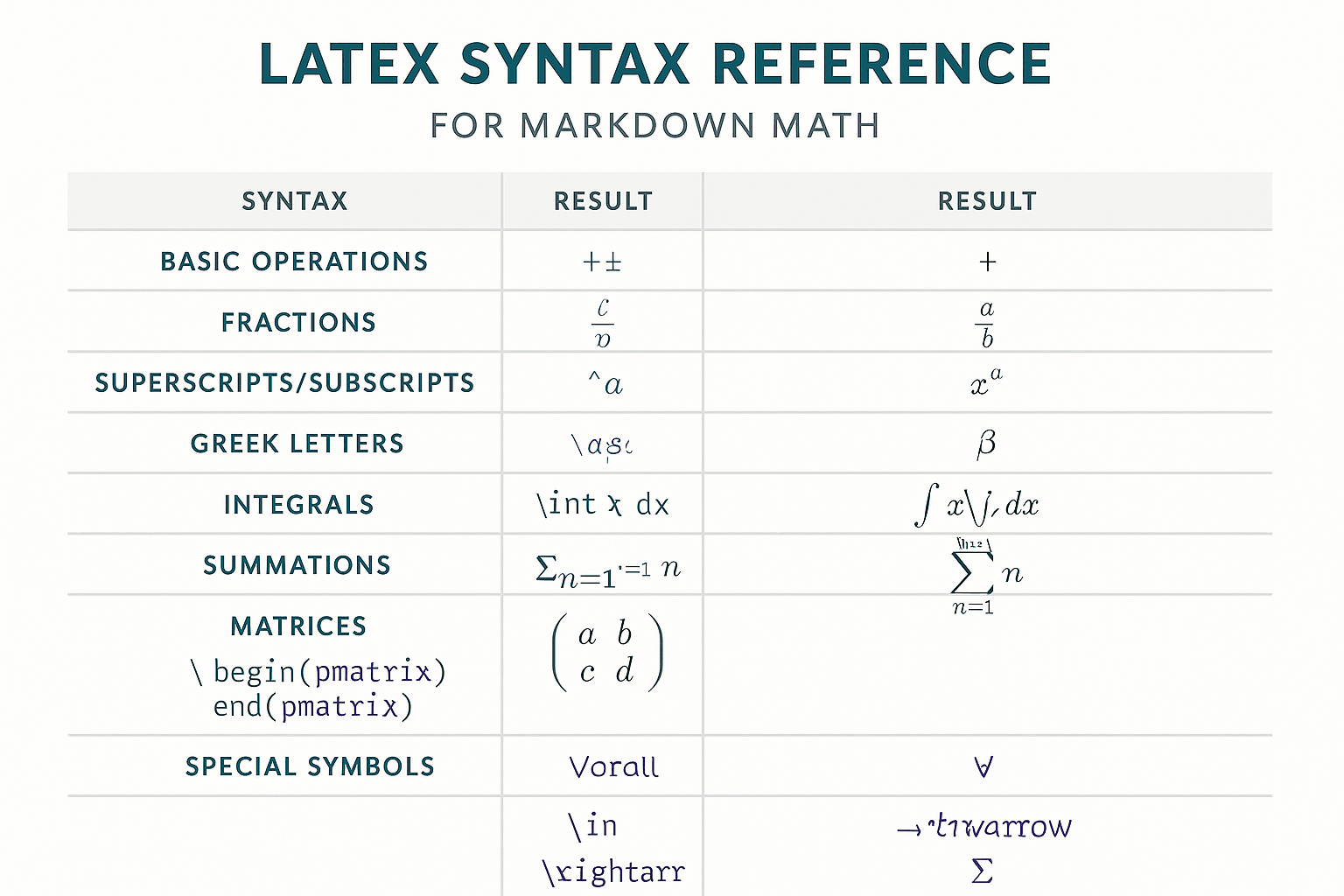
Mastering LaTeX Syntax
LaTeX, as the gold standard for mathematical typesetting, provides a powerful syntactic foundation for Markdown math formulas. A deep understanding of LaTeX math commands not only helps you create more complex and elegant mathematical expressions but also allows seamless switching between various LaTeX-supported platforms. This chapter will systematically introduce all aspects of LaTeX math syntax, from basic commands to advanced structures, equipping you with comprehensive mathematical expression capabilities.
Basic LaTeX Math Commands
LaTeX math commands follow a set of strict yet elegant syntax rules. Each command starts with a backslash, followed by the command name, and some commands require parameters to specify specific behaviors. Understanding how these basic commands work is key to mastering complex mathematical expressions.
Text and Font Control
In math mode, text is handled significantly differently than in regular text mode. By default, letters in math mode are rendered in italics, conforming to the traditional representation of mathematical variables. However, in some cases, we need to insert upright text or special fonts into math formulas.
Inserting Upright Text: When explanatory text needs to be added to a formula, use the \text{} command:
$$
P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \text{ (Bayes' Theorem)}
$$
This command ensures that the text in parentheses is displayed in upright form with proper spacing. For multilingual environments, the \text{} command correctly handles text in different languages like Chinese and English.
Math Font Variations: LaTeX provides various math fonts to represent different types of mathematical objects:
\mathbb{}: Blackboard bold, often used for number sets, e.g.,\mathbb{R}for real numbers\mathcal{}: Calligraphic letters, often used for sets or spaces, e.g.,\mathcal{F}for function spaces\mathfrak{}: Fraktur, used in certain branches of mathematics\mathbf{}: Bold, used for vectors or matrices\mathrm{}: Upright, used for function names or constants
Superscripts, Subscripts, and Modifiers
Superscripts and subscripts are the most commonly used elements in mathematical expressions, representing exponents, indices, derivatives, and other important concepts. LaTeX provides flexible and powerful syntax for superscripts and subscripts.
Basic Superscript and Subscript Syntax:
- Superscripts use
^:x^2means x squared - Subscripts use
_:x_1means the first element of x - Combined use:
x_1^2means x₁ squared
Complex Superscripts and Subscripts: When superscripts or subscripts contain multiple characters, curly braces are needed for grouping:
$$
x^{2n+1} + y_{i,j}^{(k)} = \sum_{i=1}^{n} a_i x^i
$$
This example shows the correct way to write multi-character superscripts and subscripts and their application in complex expressions.
Modifiers and Accents: LaTeX provides a rich set of modifiers to represent various mathematical concepts:
- Hat:
\hat{x}for estimates or unit vectors - Tilde:
\tilde{x}for approximate values - Bar:
\bar{x}for averages - Dot:
\dot{x}for time derivatives - Double dot:
\ddot{x}for second-order time derivatives - Vector arrow:
\vec{x}for vectors
Advanced Mathematical Structures
As the complexity of mathematical expressions increases, more advanced structures are needed to organize and display mathematical content. LaTeX provides a complete toolkit to handle everything from simple fractions to complex multi-line equation systems.
Advanced Usage of Fractions and Roots
Fractions are among the most basic concepts in mathematics. LaTeX's fraction syntax supports not only simple numerical fractions but also fraction structures containing complex expressions.
Nested Fractions: In some mathematical expressions, the numerator or denominator itself may be a fraction, creating a nested structure:
$$
\frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{x}}}}
$$
Such continued fractions often appear in number theory and approximation theory. LaTeX automatically adjusts the size of fractions at each level to ensure the overall expression remains readable.
Complex Radicals: Beyond basic square roots and nth roots, LaTeX supports more complex radical expressions:
$$
\sqrt[3]{\frac{x^2 + y^2}{x - y}} = \sqrt{\sqrt[4]{a^2 + b^2}}
$$
Fraction Size Control: In some cases, you may need to control the display size of fractions. LaTeX provides several commands for this purpose:
\dfrac{}{}: Forces display-style fraction size\tfrac{}{}: Forces text-style fraction size\cfrac{}{}: Special format for continued fractions
Summations, Integrals, and Limits
Summations, integrals, and limits in mathematical analysis are essential tools for expressing mathematical ideas. LaTeX provides specialized syntax support for these concepts, producing professional and aesthetically pleasing displays.
Using Summation Symbols:
$$
\sum_{i=1}^{n} i^2 = \frac{n(n+1)(2n+1)}{6}
$$
In this example, the \sum command creates the summation symbol, with subscripts specifying the starting condition and superscripts the ending condition. LaTeX automatically adjusts the symbol size and the position of the subscripts and superscripts.
Various Forms of Integrals:
$$
\int_0^1 x^2 dx = \frac{1}{3}, \quad \iint_D f(x,y) dA, \quad \oint_C \vec{F} \cdot d\vec{r}
$$
Here, different representations of single, double, and line integrals are shown. Each type of integral has its specific symbol and usage.
Limit Expressions:
$$
\lim_{x \to 0} \frac{\sin x}{x} = 1, \quad \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e
$$
Limits are represented using the \lim command, with the arrow symbol \to indicating the approaching relationship.
Matrices and Arrays
Matrices in linear algebra are an essential part of mathematics. LaTeX provides various environments to create different types of matrix and array structures.
Basic Matrix Environment:
$$
A = \begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}
$$
The pmatrix environment creates a matrix with parentheses, where & separates columns and \\ indicates a new line.
Matrices with Different Bracket Types:
pmatrix: Parentheses()bmatrix: Square brackets[]Bmatrix: Curly braces{}vmatrix: Determinant||Vmatrix: Double vertical lines||||
Block Matrices:
$$
M = \begin{pmatrix}
A & B \\
C & D
\end{pmatrix}
$$
Block matrices are often used in advanced linear algebra. LaTeX handles such structures very well.
Special Symbols and Functions
The richness of mathematics is reflected in its vast symbol system. LaTeX includes almost all commonly used mathematical symbols, from basic operators to specialized notations for specific disciplines.
Trigonometric and Logarithmic Functions
Mathematical functions in LaTeX have dedicated commands that ensure function names are displayed in upright form with proper spacing:
Trigonometric Functions:
$$
\sin^2 x + \cos^2 x = 1, \quad \tan x = \frac{\sin x}{\cos x}
$$
Inverse Trigonometric Functions:
$$
\arcsin x, \quad \arccos x, \quad \arctan x
$$
Hyperbolic Functions:
$$
\sinh x = \frac{e^x - e^{-x}}{2}, \quad \cosh x = \frac{e^x + e^{-x}}{2}
$$
Logarithmic Functions:
$$
\log_a x = \frac{\ln x}{\ln a}, \quad \lg x = \log_{10} x
$$
Set Theory Symbols
Set theory is the foundation of modern mathematics. LaTeX provides complete support for set theory symbols:
Basic Set Operations:
$$
A \cup B, \quad A \cap B, \quad A \setminus B, \quad A^c
$$
Relation Symbols:
$$
x \in A, \quad A \subset B, \quad A \subseteq B, \quad A \supset B
$$
Special Sets:
$$
\mathbb{N}, \quad \mathbb{Z}, \quad \mathbb{Q}, \quad \mathbb{R}, \quad \mathbb{C}
$$
Logic Symbols
Mathematical logic symbols are widely used in computer science and mathematical foundations:
Logic Connectives:
$$
P \land Q, \quad P \lor Q, \quad \neg P, \quad P \implies Q, \quad P \iff Q
$$
Quantifiers:
$$
\forall x \in \mathbb{R}, \quad \exists y \in \mathbb{N}
$$
Formula Alignment and Multi-Line Expressions
When dealing with complex mathematical derivations, we often need to align multiple formulas or split a long formula across multiple lines. LaTeX provides powerful alignment environments to meet these needs.
Using the align Environment
The align environment is the most commonly used tool for handling multi-line formula alignment:
$$
\begin{align}
(x+y)^2 &= x^2 + 2xy + y^2 \\
&= x^2 + y^2 + 2xy \\
&= (x^2 + y^2) + 2xy
\end{align}
$$
In this example, the & symbol marks the alignment point, usually placed before the equal sign, ensuring all equal signs are vertically aligned.
Representing Equation Systems
Equation systems are common structures in mathematics. LaTeX provides various ways to represent them:
Using the cases Environment:
$$
f(x) = \begin{cases}
x^2 & \text{if } x \geq 0 \\
-x^2 & \text{if } x < 0
\end{cases}
$$
Linear Equation Systems:
$$
\begin{align}
2x + 3y &= 7 \\
x - y &= 1
\end{align}
$$
Mastering these advanced structures will enable you to handle almost all types of mathematical expressions, from simple algebraic operations to complex mathematical analysis, from basic geometric relationships to sophisticated abstract algebra. The power of LaTeX lies in its consistency and extensibility—once you understand the basic principles, you can easily handle various complex mathematical typesetting needs.
Platform Support Comparison
Different Markdown platforms have significantly varying levels of support for math formulas. These differences manifest not only in syntax compatibility but also in rendering quality, performance, and user experience. Understanding the characteristics and limitations of each platform is crucial for choosing the right working environment. This chapter will analyze the math formula support of mainstream platforms in detail, helping you make informed choices in different environments.
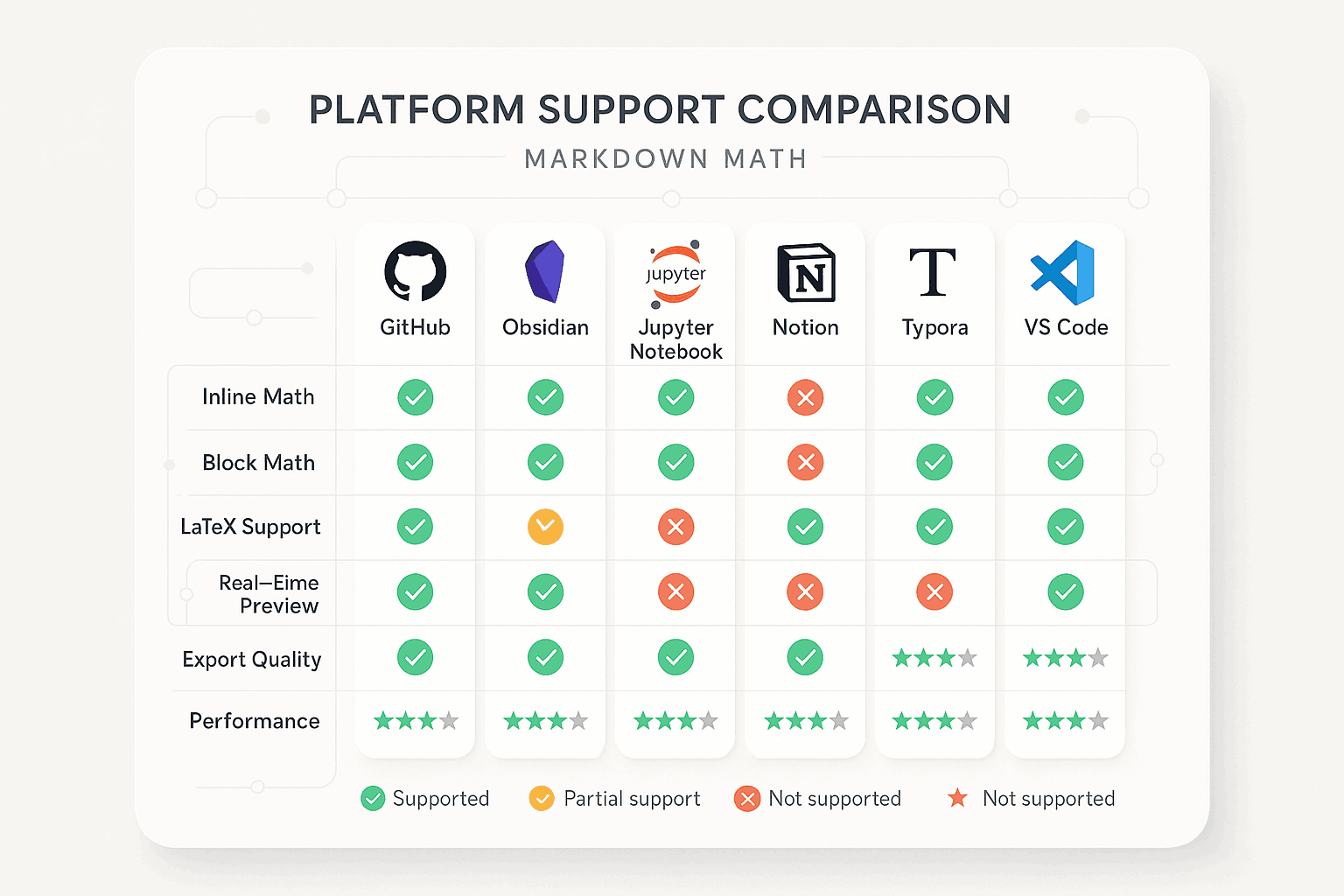
GitHub Math Formula Support
GitHub officially introduced math formula support in May 2022 [2], a major update marking an important step toward academic and technical document friendliness for code hosting platforms. GitHub's math formula implementation is based on the MathJax rendering engine, providing relatively complete LaTeX syntax support.
GitHub's Syntax Features
GitHub adopts standard dollar sign delimiter syntax, supporting both inline and block-level modes:
Inline Formulas: Enclosed by single dollar signs, e.g., $E = mc^2$
Block-level Formulas: Enclosed by double dollar signs, displayed on separate lines
GitHub's implementation strictly follows LaTeX standards, meaning formulas written in other LaTeX-supporting environments can be used directly on GitHub without modification. This compatibility is extremely important for open-source project documentation maintenance, especially when projects involve mathematical algorithms or scientific computing.
Supported Feature Range
GitHub's math formula support covers most commonly used LaTeX math commands:
Basic Mathematical Structures: Core features like fractions, radicals, superscripts/subscripts, summations, and integrals are fully supported. Complex nested structures also render correctly, meeting most technical documentation needs.
Matrices and Arrays: Various matrix environments are supported, including pmatrix, bmatrix, vmatrix, etc., capable of handling linear algebra-related expressions.
Special Symbols: Greek letters, mathematical operators, set theory symbols, and logic symbols all have good support.
Multi-line Formulas: The align environment and cases environment both work normally, supporting complex formula alignment and equation system representation.
Usage Limitations and Considerations
Despite GitHub's comprehensive math formula support, some limitations should be noted:
Rendering Performance: Since MathJax requires client-side rendering, pages containing many math formulas may experience loading delays. This is particularly noticeable in formula-dense technical documents.
Mobile Experience: On mobile devices, complex math formulas may display poorly, especially on small screens where long formulas might exceed screen boundaries.
Caching Mechanism: GitHub caches rendering results, but in some cases, formula updates may not immediately reflect on the page, requiring forced refresh to see the latest effects.
Obsidian Math Formula Features
As a professional knowledge management tool, Obsidian provides excellent math formula support. Its math formula functionality is based on MathJax implementation, supporting not only standard LaTeX syntax but also providing unique enhanced features.
Real-time Preview Experience
One of Obsidian's greatest advantages is its real-time preview functionality. In edit mode, math formulas render instantly, allowing users to see the final effect while typing. This immediate feedback greatly improves the efficiency of mathematical content creation, making it particularly suitable for academic workers who frequently edit math formulas.
Smart Hints in Edit Mode: Obsidian provides syntax highlighting and error hints when editing math formulas, helping users quickly identify and correct syntax errors. When formula syntax is incorrect, the editor displays obvious error indicators and provides correction suggestions when possible.
Optimized Rendering in Preview Mode: In preview mode, Obsidian uses optimized rendering algorithms to ensure both display quality and performance of math formulas reach optimal states. Complex formulas maintain clear display effects.
Advanced Feature Support
Obsidian supports some advanced LaTeX features that may not be available on other platforms:
Custom Macro Definitions: Users can define their own LaTeX macros to simplify common formula input. For example, defining \newcommand{\R}{\mathbb{R}} for quick input of real number set symbols.
Chemical Formula Support: Through the mhchem extension, Obsidian can render chemical equations and molecular structures, very useful for chemistry and biology-related notes.
Chart Integration: Obsidian supports integrating math formulas with chart tools, allowing mixed use of mathematical expressions and visualization charts in the same document.
Plugin Ecosystem
Obsidian's rich plugin ecosystem provides further extension possibilities for math formula functionality:
LaTeX Suite Plugin: Provides more convenient LaTeX input experience, including shortcuts, auto-completion, and template functions.
Math Booster Plugin: Enhances math formula editing and display functions, providing additional mathematical symbols and formatting options.
Export Plugin: Supports exporting notes containing math formulas to PDF, HTML, and other formats while maintaining formula integrity.
Jupyter Notebook Math Rendering
As the standard tool for data science and scientific computing, Jupyter Notebook has natural needs and excellent support for math formulas. Its math formula functionality serves not only document explanations but also as an important bridge between code and mathematical theory.
Seamless Integration with Code
Jupyter Notebook's unique feature is its ability to perfectly combine math formulas with executable code:
Theory-Practice Integration: Writing mathematical theory in Markdown cells and implementing corresponding algorithms in code cells makes learning and applying mathematical concepts more intuitive.
Dynamic Formula Generation: LaTeX formula strings can be dynamically generated through Python code and then rendered in Markdown cells. This is particularly useful for parameterized mathematical expressions.
Mathematical Representation of Computational Results: Symbolic computation libraries like SymPy can directly output LaTeX-formatted mathematical expressions, seamlessly integrating into Notebook's display system.
Professional Support for Scientific Computing
Jupyter Notebook's widespread use in scientific computing provides special optimization for math formulas:
NumPy and SciPy Integration: Numerical computation results can be directly converted to math formula displays, facilitating result presentation and analysis.
Matplotlib Integration: Math formulas and scientific charts can be mixed in the same Notebook, creating complete scientific reports.
Multimedia Support: Beyond static math formulas, Jupyter supports interactive mathematical visualizations, creating dynamic mathematical demonstrations through widgets.
Export and Sharing Features
Jupyter Notebook provides various export options ensuring math formulas display correctly in different formats:
PDF Export: Generates high-quality PDF documents through LaTeX engines, with math formula rendering quality reaching publication level.
HTML Export: Generates HTML files containing MathJax that can display math formulas correctly in any modern browser.
Slide Mode: Supports converting Notebooks to presentations, with math formulas maintaining clear display during presentations.
Notion Math Formula Usage
As a modern collaboration tool, while Notion isn't specifically designed for mathematical content, its math formula functionality can meet most users' basic needs. Notion's math formulas are based on KaTeX implementation, providing fast rendering performance and good user experience.
User-Friendly Input Methods
Notion has made many optimizations to the math formula input experience, lowering the barrier to entry:
Visual Editor: Notion provides a visual editing interface for math formulas, allowing users to insert common mathematical symbols by clicking buttons without memorizing complex LaTeX commands.
Real-time Preview: When editing math formulas, Notion displays rendering results in real-time, allowing users to immediately see the final effect.
Templates and Shortcuts: Notion provides templates for common math formulas, allowing users to quickly insert fractions, radicals, integrals, and other common structures.
Mathematical Support for Collaboration Features
As a collaboration platform, Notion's math formula functionality particularly considers team usage scenarios:
Comments and Discussions: Team members can comment and discuss content containing math formulas, supporting collaborative editing of mathematical content.
Version History: Notion saves editing history of math formulas, allowing tracking of formula modification processes, particularly important for academic collaboration.
Permission Control: Different user access and editing permissions for mathematical content can be set, ensuring security of important formulas.
Feature Limitations and Alternatives
While Notion's math formula functionality is practical, it still has some limitations compared to professional mathematical tools:
Syntax Support Range: KaTeX-based implementation means some advanced LaTeX features may not be supported, especially specialized mathematical packages and custom commands.
Complex Formula Handling: For very complex mathematical expressions, Notion's performance may be affected, with potentially slower rendering speeds.
Export Format Limitations: When exporting documents, math formula formats may change, especially when exporting to certain formats where formula information might be lost.
Other Mainstream Platform Comparisons
Besides the major platforms mentioned above, many other tools provide varying degrees of math formula support:
Typora
As a WYSIWYG Markdown editor, Typora provides excellent math formula support:
Instant Rendering: When inputting math formulas, Typora immediately converts LaTeX code to rendered formulas, providing true WYSIWYG experience.
Export Quality: Typora's PDF export function can generate high-quality math formulas, suitable for creating formal documents.
Theme Support: Different themes have different style settings for math formulas, allowing users to choose the most suitable display effects.
VS Code
With appropriate extensions, VS Code can provide powerful math formula support:
Markdown Preview Enhanced: This extension adds complete math formula rendering functionality to VS Code, supporting real-time preview.
LaTeX Workshop: Specialized LaTeX extension providing complete LaTeX editing and compilation environment.
Custom Configuration: Users can configure math formula rendering engines and display styles according to their needs.
Online Editors
Many online Markdown editors also provide math formula support:
StackEdit: Browser-based Markdown editor supporting real-time math formula preview.
Dillinger: Simple online editor providing basic math formula functionality.
HackMD: Collaborative Markdown editor supporting team collaborative editing of documents containing math formulas.
Platform Selection Recommendations
Choosing the right platform requires considering multiple factors:
Usage Scenarios: Academic writing might be better suited for Obsidian or Jupyter Notebook, while team collaboration might be better suited for Notion or GitHub.
Technical Requirements: Users with high requirements for LaTeX syntax support completeness should choose MathJax-based platforms.
Performance Needs: Scenarios requiring fast rendering can consider KaTeX-based platforms.
Integration Needs: Scenarios requiring integration with code or other tools should consider Jupyter Notebook or VS Code.
Understanding the characteristics and limitations of each platform helps you make optimal choices in different working environments, ensuring both quality and efficiency of mathematical content reach optimal states.
Rendering Engine Deep Dive
The final display effect of math formulas largely depends on the underlying rendering engine. Currently, the mainstream rendering engines are mainly MathJax and KaTeX, each with distinct characteristics and applicable scenarios. Understanding the working principles and features of these rendering engines helps us make optimal choices in different environments and optimize math formula display effects.

MathJax vs KaTeX Comparison
MathJax and KaTeX represent two different development directions in math formula rendering technology. MathJax pursues feature completeness and compatibility, while KaTeX focuses on performance and speed optimization.
MathJax Features and Advantages
As one of the earliest web math formula rendering engines, MathJax has become very mature through years of development:
Feature Completeness: MathJax supports almost all LaTeX math commands, including many advanced features and extension packages. This comprehensive support allows complex academic documents to seamlessly migrate from LaTeX environments to web environments.
Multi-format Support: Besides LaTeX, MathJax also supports MathML and AsciiMath input formats, providing flexible choices for users with different backgrounds.
High-quality Rendering: MathJax's rendering quality approaches professional mathematical typesetting software, maintaining excellent visual effects especially when handling complex mathematical structures.
Configurability: MathJax provides rich configuration options, allowing users to adjust rendering behavior, font selection, output format, and many other aspects as needed.
KaTeX Features and Advantages
KaTeX, developed by Khan Academy, is specifically optimized for web environment performance needs:
Rendering Speed: KaTeX's greatest advantage is its extremely fast rendering speed. Compared to MathJax, KaTeX renders an order of magnitude faster, which is particularly important for pages containing many math formulas.
Server-side Rendering: KaTeX supports server-side pre-rendering, allowing math formula processing to be completed before page loading, further enhancing user experience.
Lightweight Design: KaTeX's file size is much smaller than MathJax, reducing network transmission burden, particularly suitable for mobile devices and poor network conditions.
Modern Architecture: KaTeX adopts more modern JavaScript architecture, integrating more smoothly with modern frontend frameworks.
Performance and Compatibility Analysis
When choosing a rendering engine, performance and compatibility are the two most important considerations. Different application scenarios have different requirements for these two aspects.
Performance Comparison Testing
In actual use, rendering engine performance differences mainly manifest in the following aspects:
Initial Loading Time: KaTeX's library file size is about 100KB, while MathJax's complete version may exceed 1MB. In limited network conditions, this difference significantly affects page first-load speed.
Formula Rendering Speed: For pages containing 100 math formulas, KaTeX typically completes rendering in tens of milliseconds, while MathJax may need hundreds of milliseconds or longer.
Memory Usage: KaTeX's memory footprint is typically 30-50% lower than MathJax, particularly important for resource-constrained devices.
Compatibility Considerations
Compatibility mainly involves LaTeX syntax support levels and browser compatibility:
LaTeX Syntax Support: MathJax supports far more LaTeX commands than KaTeX. For users using advanced LaTeX features, MathJax may be the only choice.
Browser Compatibility: Both engines support modern browsers, but MathJax has better support for older browser versions.
Mobile Device Support: KaTeX typically performs better on mobile devices, especially on low-end devices.
Selection Recommendations
Based on different usage scenarios, we can provide the following selection recommendations:
Choose MathJax when:
- Complete LaTeX syntax support is needed
- Documents contain complex mathematical structures
- Extremely high rendering quality requirements
- Multiple input format support is needed
Choose KaTeX when:
- High rendering speed requirements
- Pages contain many math formulas
- Primarily used on mobile devices
- Server-side rendering is needed
Practical Application Cases
Theoretical knowledge needs to be truly mastered through practical application. This chapter will demonstrate how to effectively use Markdown math formulas in real work through several typical application scenarios. These cases cover various needs from academic writing to technical documentation, providing directly referenceable practical experience for readers.
Academic Paper Writing
Academic papers have the strictest requirements for math formulas, needing not only accurate mathematical expressions but also formatting that conforms to academic standards.
Representing Theorems and Proofs
In mathematical papers, structures like theorems, lemmas, and proofs need clear identification:
**Theorem 1**: For any real numbers $a, b, c$, if $a^2 + b^2 = c^2$, then there exists a right triangle with side lengths $a, b, c$.
**Proof**: Let the three sides of a triangle be $a, b, c$, where $c$ is the longest side. According to the law of cosines:
$$
c^2 = a^2 + b^2 - 2ab\cos C
$$
If $a^2 + b^2 = c^2$, then:
$$
2ab\cos C = 0
$$
Since $a, b > 0$, we have $\cos C = 0$, i.e., $C = 90°$. Therefore, the triangle is a right triangle. $\square$
Handling Complex Equation Systems
Academic papers often need to display complex equation systems:
$$
\begin{align}
\frac{\partial u}{\partial t} &= \alpha \frac{\partial^2 u}{\partial x^2} + f(x,t) \\
u(0,t) &= g_1(t) \\
u(L,t) &= g_2(t) \\
u(x,0) &= h(x)
\end{align}
$$
This format clearly displays partial differential equations with their boundary conditions and initial conditions.
Technical Documentation Writing
Math formulas in technical documentation are typically used to explain algorithm principles, performance analysis, or parameter calculations.
Algorithm Complexity Analysis
**Time Complexity Analysis**:
The average time complexity of quicksort is $O(n \log n)$, where $n$ is the number of elements to be sorted.
In the worst case, when the input array is already sorted, quicksort degrades to $O(n^2)$ complexity:
$$
T(n) = T(n-1) + O(n) = O(n^2)
$$
In the average case, the divide-and-conquer strategy results in:
$$
T(n) = 2T(n/2) + O(n) = O(n \log n)
$$
Machine Learning Formulas
In machine learning documentation, math formulas explain model principles:
**Linear Regression Model**:
Hypothesis function: $h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n$
Cost function:
$$
J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2
$$
Gradient descent update rule:
$$
\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta)
$$
Creating Teaching Materials
Teaching materials need to introduce mathematical concepts progressively, with formulas presented clearly and understandably.
Concept Explanation and Examples
**Definition of Derivative**:
The derivative of function $f(x)$ at point $x_0$ is defined as:
$$
f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}
$$
**Example**: Find the derivative of $f(x) = x^2$ at $x = 2$.
**Solution**:
$$
\begin{align}
f'(2) &= \lim_{h \to 0} \frac{(2+h)^2 - 2^2}{h} \\
&= \lim_{h \to 0} \frac{4 + 4h + h^2 - 4}{h} \\
&= \lim_{h \to 0} \frac{4h + h^2}{h} \\
&= \lim_{h \to 0} (4 + h) \\
&= 4
\end{align}
$$
Advanced Techniques and Best Practices
Mastering basic syntax is just the beginning. True professional level is reflected in the application of advanced techniques and adherence to best practices. This chapter will share some advanced techniques for improving math formula quality and efficiency.
Organizing Complex Formulas
When facing very complex mathematical expressions, proper organization and decomposition are key:
Using Intermediate Variables
Let $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$, $B = \begin{pmatrix} e & f \\ g & h \end{pmatrix}$
Then the matrix product is:
$$
AB = \begin{pmatrix}
ae + bg & af + bh \\
ce + dg & cf + dh
\end{pmatrix}
$$
Showing Derivation Steps
$$
\begin{align}
\int_0^1 x^2 e^x dx &= \left[ x^2 e^x \right]_0^1 - \int_0^1 2x e^x dx \\
&= e - 2\int_0^1 x e^x dx \\
&= e - 2\left( \left[ x e^x \right]_0^1 - \int_0^1 e^x dx \right) \\
&= e - 2(e - (e - 1)) \\
&= e - 2
\end{align}
$$
Performance Optimization Techniques
In documents containing many math formulas, performance optimization becomes important:
Avoiding Overly Complex Nesting
// Not recommended: excessive nesting
$$
\frac{\frac{\frac{a}{b}}{\frac{c}{d}}}{\frac{\frac{e}{f}}{\frac{g}{h}}}
$$
// Recommended: using intermediate variables
Let $x = \frac{a}{b} \cdot \frac{d}{c}$, $y = \frac{e}{f} \cdot \frac{h}{g}$
Then the original expression = $\frac{x}{y}$
Proper Use of Formula Numbering
Important formulas should be numbered for reference:
$$
E = mc^2 \tag{1}
$$
According to formula (1), we can calculate...
Cross-Platform Compatibility
Ensuring math formulas display correctly on different platforms:
Avoiding Platform-Specific Extensions
// Avoid using platform-specific extension commands
// Use standard LaTeX syntax to ensure compatibility
Testing and Verification
Before publishing, test math formula display effects on target platforms to ensure no rendering issues.
Tools and Resource Recommendations
The right tools can significantly improve the efficiency and quality of math formula writing.
Online Editor Recommendations
ToMarkdown.org: As a professional Markdown tool platform, ToMarkdown.org not only provides excellent math formula editing experience but also has powerful format conversion capabilities. Particularly its HTML to Markdown conversion ability can intelligently handle complex documents containing math formulas, providing great convenience for users' content migration.
Upmath: Specialized online math formula editor providing real-time preview and LaTeX code generation functionality.
CodeCogs: Provides online math formula editing and image generation services, suitable for embedding formulas in environments that don't support LaTeX.
Desktop Tools
Typora: WYSIWYG Markdown editor with excellent math formula support.
Obsidian: Knowledge management tool providing powerful math formula functionality and plugin ecosystem.
VS Code + Extensions: Through extensions like Markdown Preview Enhanced, VS Code can provide professional math formula editing environments.
Learning Resources
LaTeX Math Symbol Tables: Complete LaTeX math symbol references, essential materials for writing complex formulas.
MathJax Documentation: Official documentation providing detailed syntax explanations and configuration guides.
KaTeX Support Tables: Lists all LaTeX commands supported by KaTeX, helpful for ensuring compatibility.
Troubleshooting Guide
Various problems may be encountered when using Markdown math formulas. This chapter provides diagnosis and solutions for common issues.
Common Problem Solutions
Formulas Not Displaying:
- Check if dollar signs are properly paired
- Confirm if the platform supports math formulas
- Check if LaTeX syntax is correct
Rendering Errors:
- Check if special characters need escaping
- Confirm if used commands are supported
- Check if nested structures are correct
Performance Issues:
- Reduce the number of formulas on the page
- Use faster rendering engines
- Consider server-side pre-rendering
Debugging Techniques
Step-by-step Simplification: When complex formulas have problems, gradually simplify formula content to locate the issue.
Syntax Validation: Use online LaTeX editors to validate syntax correctness.
Platform Testing: Test formula display effects on different platforms to ensure compatibility.
Summary and Outlook
Markdown math formulas, as an important component of modern technical writing, have become indispensable tools in academic communication, technical documentation, and educational materials. Through studying this guide, you should have mastered a complete skill system from basic syntax to advanced applications.
Best Practices Summary
- Choose Appropriate Platforms: Select the most suitable Markdown platform and rendering engine based on specific needs
- Follow Standard Syntax: Use standard LaTeX syntax to ensure cross-platform compatibility
- Focus on Readability: Properly organize complex formulas to improve document readability
- Performance Optimization: Pay attention to performance optimization in formula-dense documents
- Testing and Verification: Thoroughly test formula display effects before publishing
Future Development Trends
Math formula rendering technology continues to evolve, with possible future trends including:
Faster Rendering Speed: New rendering engines will further improve performance Better Mobile Support: Optimizations for mobile devices will become more complete AI-Assisted Writing: Artificial intelligence may help automatically generate and optimize math formulas Richer Interactivity: Math formulas may support more interactive features
Mastering Markdown math formulas is not only an improvement in technical skills but also an important component of modern academic and technical communication capabilities. As technology continues to develop, the value of this skill will become increasingly prominent.
References
[1] GitHub Blog. "Math support in Markdown". https://github.blog/2022-05-19-math-support-in-markdown/
[2] GitHub Docs. "Writing mathematical expressions". https://docs.github.com/en/get-started/writing-on-github/working-with-advanced-formatting/writing-mathematical-expressions
[3] MathJax Documentation. https://docs.mathjax.org/
[4] KaTeX Documentation. https://katex.org/docs/
[5] LaTeX Mathematics. https://en.wikibooks.org/wiki/LaTeX/Mathematics
[6] Jupyter Book Math Guide. https://jupyterbook.org/content/math.html
[7] Obsidian Math Support. https://help.obsidian.md/How+to/Format+your+notes#Math
[8] ToMarkdown.org Platform. https://tomarkdown.org